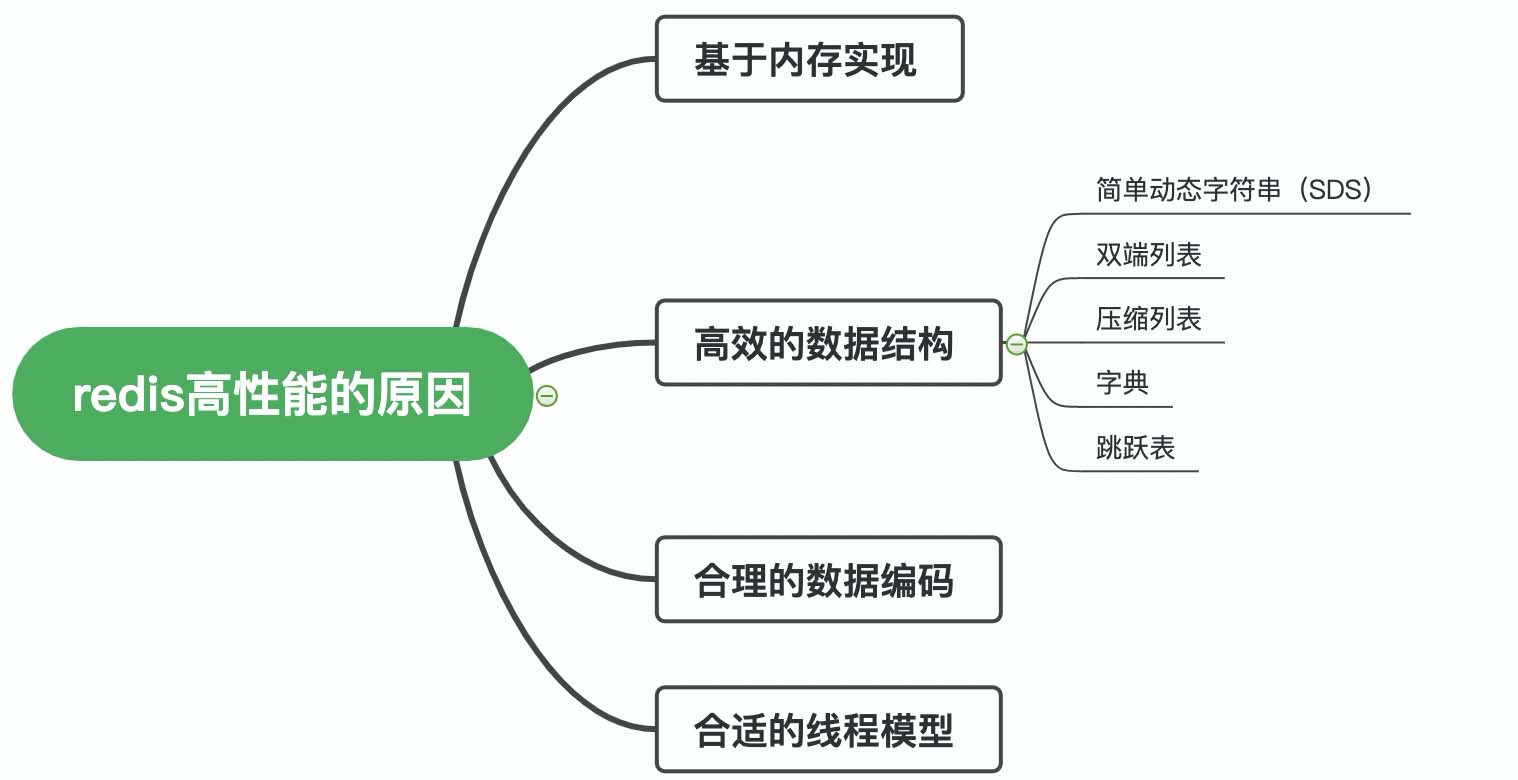
一、基于内存实现
Redis 是基于内存的数据库,那不可避免的就要与磁盘数据库做对比。
对于磁盘数据库来说,是需要将数据读取到内存里的,这个过程会受到磁盘 I/O 的限制。
而对于内存数据库来说,本身数据就存在于内存里,也就没有了这方面的开销。
二、高效的数据结构
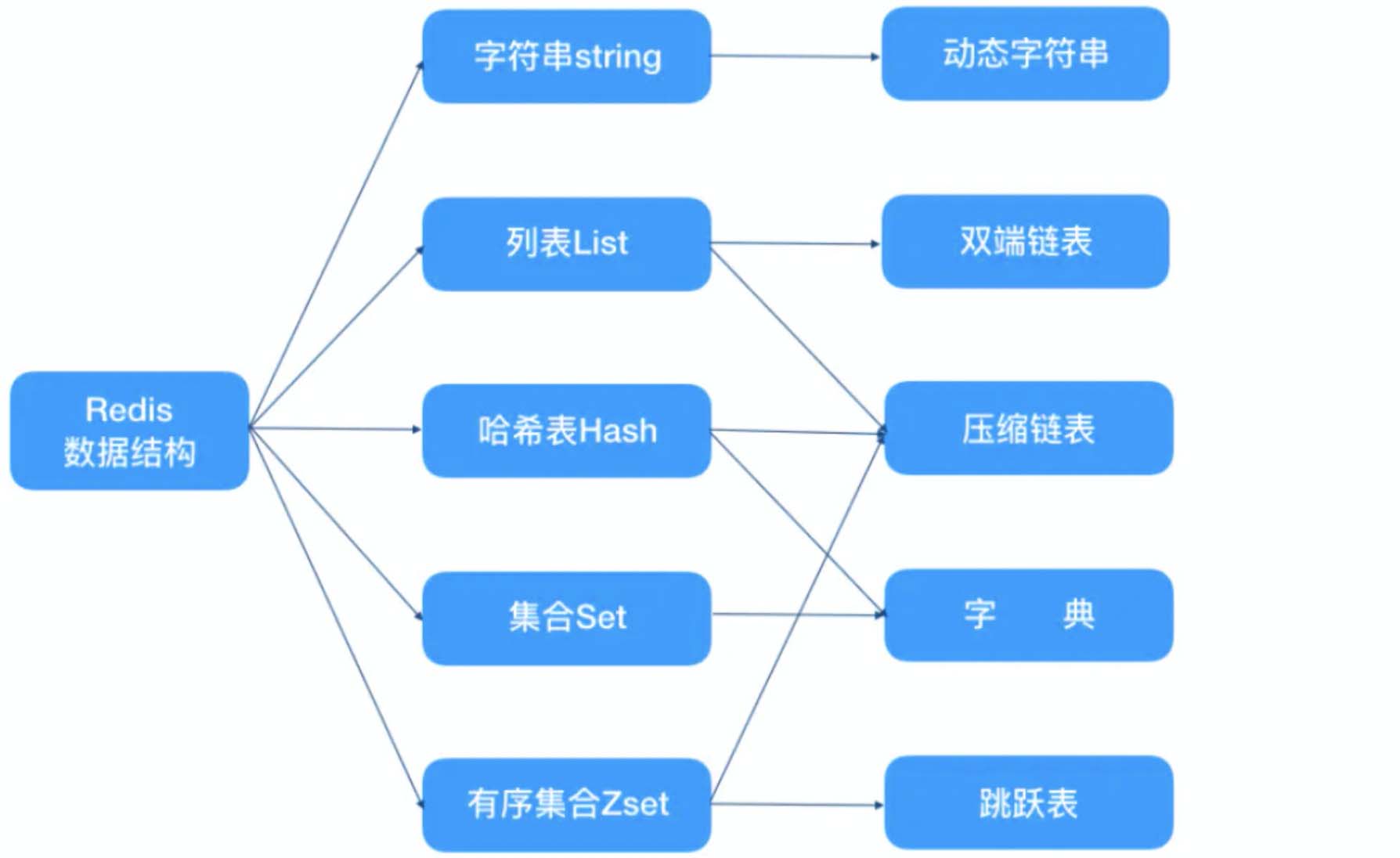
Redis 中有多种数据类型,每种数据类型的底层都由一种或多种数据结构来支持。
正是因为有了这些数据结构,Redis 在存储与读取上的速度才不受阻碍。
1. 简单动态字符串(SDS)
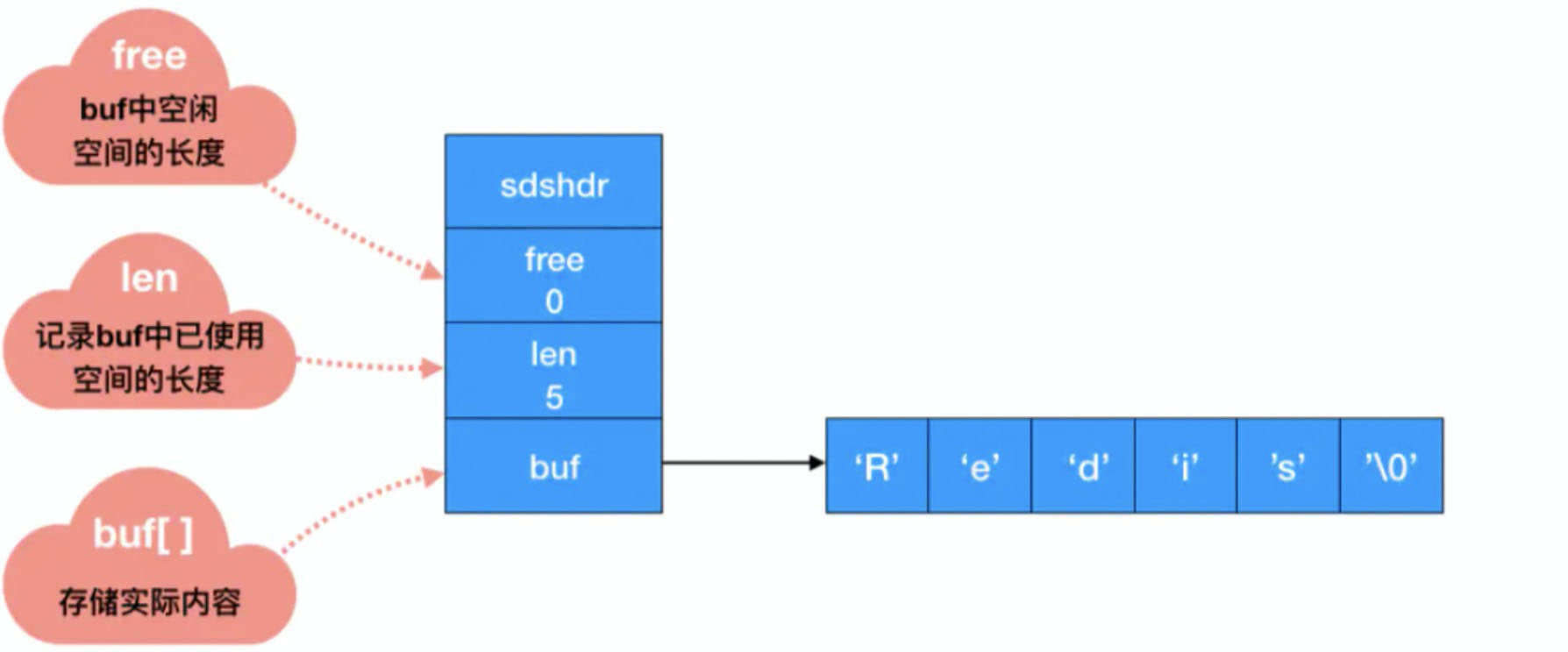
(1)字符串长度处理
用一个 len 字段记录当前字符串的长度。想要获取长度只需要获取 len 字段即可,时间复杂度为 O(1)。
(2)内存重新分配
修改字符串的时候会重新分配内存。修改地越频繁,内存分配也就越频繁。而内存分配是会消耗性能的,那么性能下降在所难免。而 Redis 中会涉及到字符串频繁的修改操作,于是 SDS 实现了两种优化策略:
- - 空间预分配
对 SDS 修改及空间扩充时,除了分配所必须的空间外,还会额外分配未使用的空间。
具体分配规则是这样的:SDS 修改后,len 长度小于 1M,那么将会额外分配与 len 相同长度的未使用空间。如果修改后长度大于 1M,那么将分配1M的使用空间。
- - 惰性空间释放
当然,有空间分配对应的就有空间释放。
SDS 缩短时,并不会回收多余的内存空间,而是使用 free 字段将多出来的空间记录下来。如果后续有变更操作,直接使用 free 中记录的空间,减少了内存的分配。
(3)二进制安全
读取字符串遇到 ‘\0’ 会结束,那 ‘\0’ 之后的数据就读取不上了。但在 SDS 中,是根据 len 长度来判断字符串结束的,二进制安全的问题就解决了。
2. 双端链表
- - 头尾节点
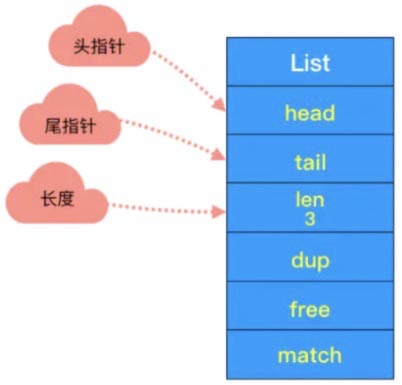
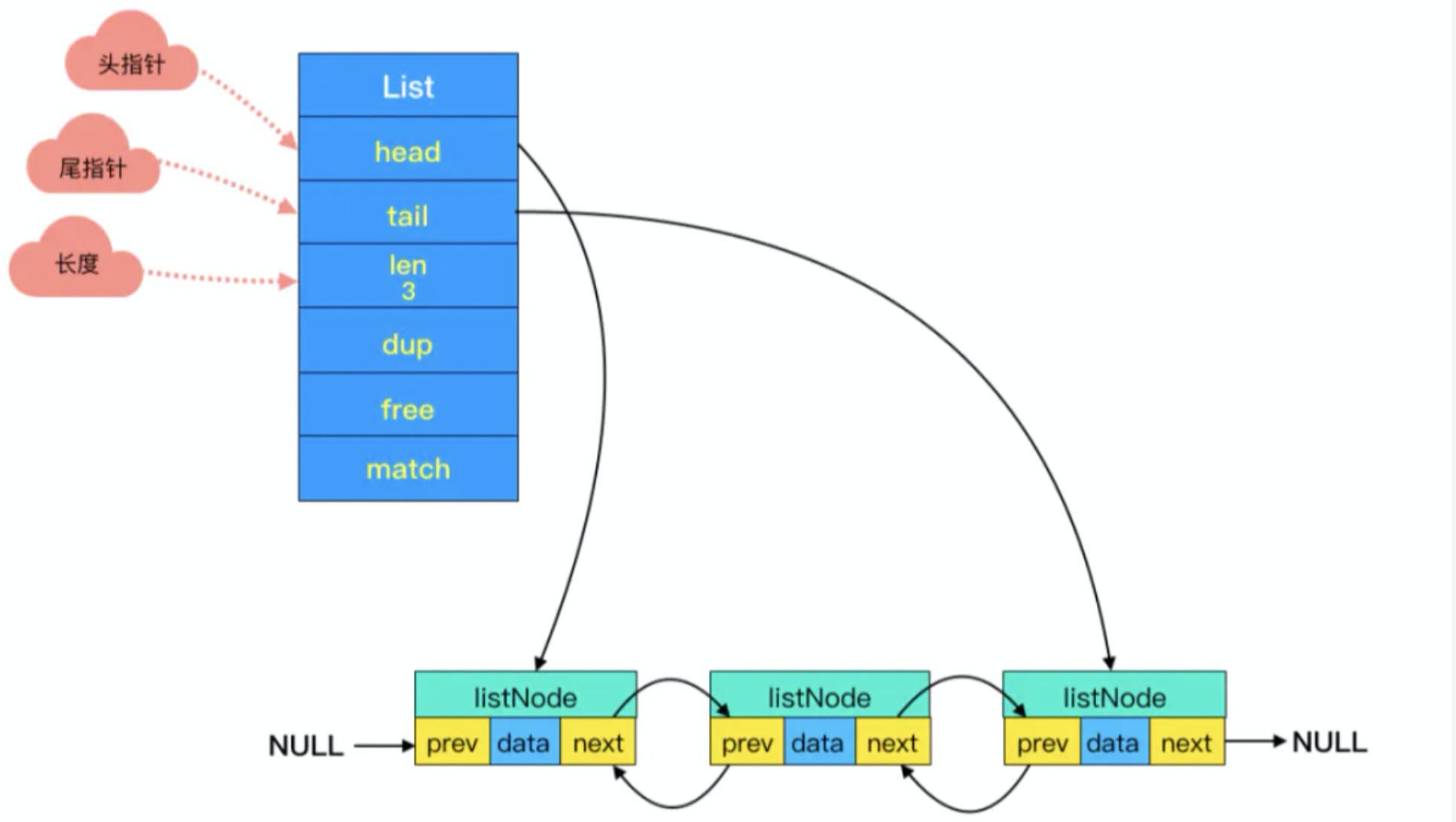
头节点里有 head 和 tail 两个参数,分别指向头节点和尾节点。这样的设计能够对双端节点的处理时间复杂度降至 O(1) ,对于队列和栈来说再适合不过。同时链表迭代时从两端都可以进行。
- - 链表长度
头节点里同时还有一个参数 len,和上边提到的 SDS 里类似,这里是用来记录链表长度的。因此获取链表长度时不用再遍历整个链表,直接拿到 len 值就可以了,这个时间复杂度是 O(1)。
- - 每个节点

链表里每个节点都带有两个指针,prev 指向前节点,next 指向后节点。这样在时间复杂度为 O(1) 内就能获取到前后节点。
- - 链表结构
3. 压缩列表
如果在一个链表节点中存储一个小数据,比如一个字节。那么对应的就要保存头节点,前后指针等额外的数据。
这样就浪费了空间,同时由于反复申请与释放也容易导致内存碎片化。这样内存的使用效率就太低了。Redis为了节约内存开发了压缩列表。
压缩列表结构

参数说明:
- zlbytes:记录整个压缩列表占用的内存字节数。
- zltail:记录压缩列表表尾节点距离压缩列表起始地址有多少字节。
- zllen:记录了压缩列表包含的节点数量。
- entryN:压缩列表的节点,节点长度由节点保存的内容决定。
- zlend:特殊值0xFF(十进制255),用于标记压缩列表的末端。
4. 字典
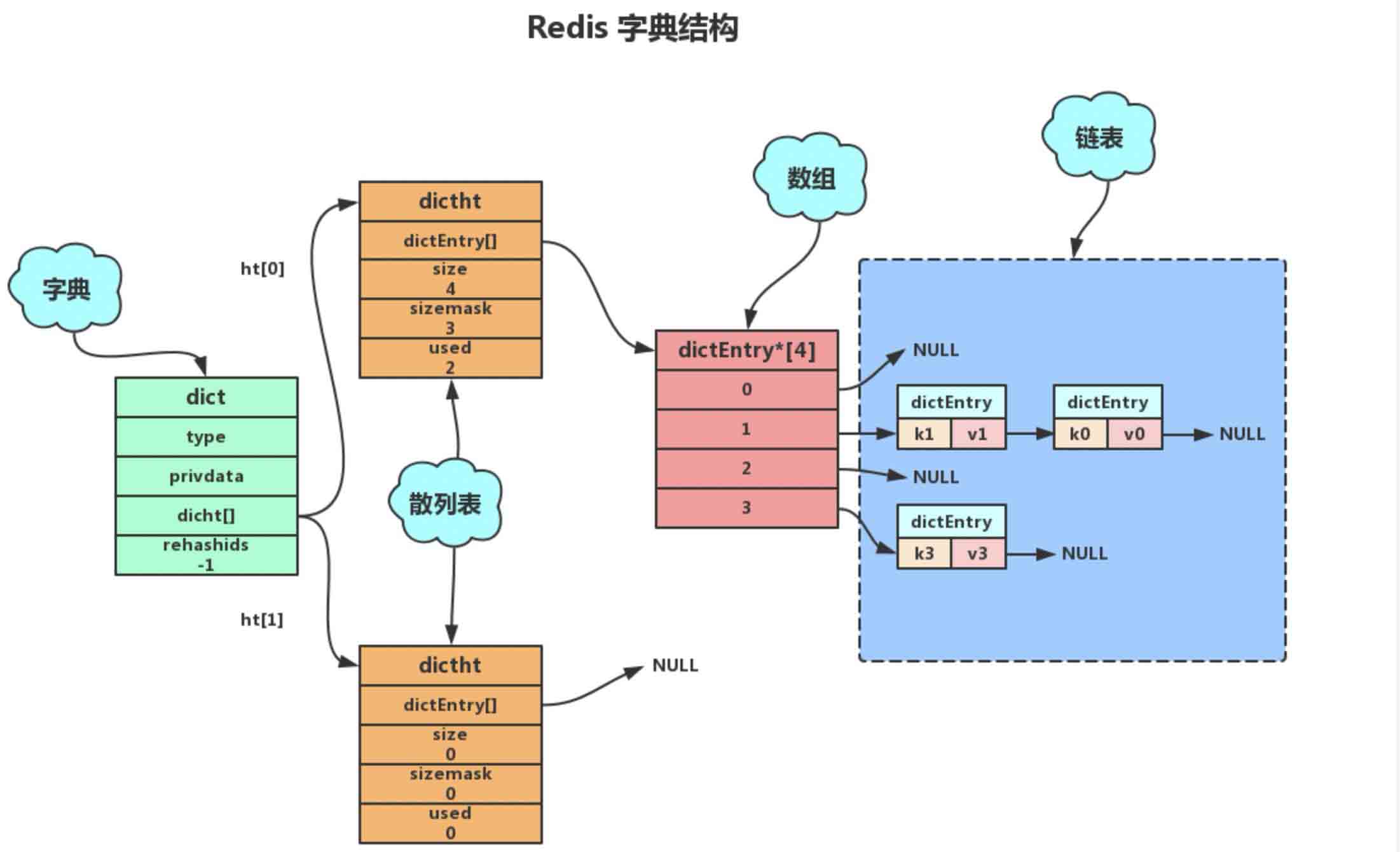
dict结构体是字典中最顶层的结构体,用于指向两个哈希表,两个哈希表是为了在扩容时使用
hash扩容:
- 1 创建ht[1],长度= len(ht[0]) * 2
- 2 将ht[0]上的数据rehash到ht[1]上,即重新计算哈希地址
- 3 释放ht[0],将ht[1]设置为ht[0],然后创建新的ht[1]
5. 跳跃表
调表的结构:
由多层链表构成,每层之间部分节点相连,且每层链表的数据都是有序的
最底层的链表是双向的,且包含所有元素,可实现类似二分查找,
在调表中的查找次数接近层数,时间复杂度为O(logn)
用随机化来决定哪些节点需要上浮

跳表中的查找:
类似二分查找,从最顶层开始查找,大数向右查找,小数向左查找
如查找17,查找路径为 13 -> 46 -> 22 -> 17
因为17>13(L3),就在L3中往后走,发现17<46(L3),
就通过13(L3)到达了13(L2),然后往后走发现17<22(L2),
就通过13(L2)往下达到了13(L1),然后往后走就遇到了17
查找35 13 -> 46 -> 22 -> 46 -> 35
查找 54 13 -> 46 -> 54
跳表中的插入:
1 先在最底层链表中找到合适的位置,并插入
2 然后用抛硬币的方式决定它是需要上浮的次数
假如此时链表共3层,需要抛两次硬币,来决定它上浮几次
跳表与平衡树、哈希表的比较
1 skiplist和各种平衡树(如AVL、红黑树等)的元素是有序排列的,而哈希表不是有序的。
因此,在哈希表上只能做单个key的查找,不适宜做范围查找。所谓范围查找,指的是查找那些大小在指定的两个值之间的所有节点。
2 在做范围查找的时候,平衡树比skiplist操作要复杂。
在平衡树上,我们找到指定范围的小值之后,还需要以中序遍历的顺序继续寻找其它不超过大值的节点。
如果不对平衡树进行一定的改造,这里的中序遍历并不容易实现。
而在skiplist上进行范围查找就非常简单,只需要在找到小值之后,对第1层链表进行若干步的遍历就可以实现。
3 平衡树的插入和删除操作可能引发子树的调整,逻辑复杂,
而skiplist的插入和删除只需要修改相邻节点的指针,操作简单又快速。
4 从内存占用上来说,skiplist比平衡树更灵活一些。
一般来说,平衡树每个节点包含2个指针(分别指向左右子树),而skiplist每个节点包含的指针数目平均为1/(1-p),具体取决于参数p的大小。如果像Redis里的实现一样,取p=1/4,那么平均每个节点包含1.33个指针,比平衡树更有优势。
5 查找单个key,skiplist和平衡树的时间复杂度都为O(log n),大体相当;
而哈希表在保持较低的哈希值冲突概率的前提下,查找时间复杂度接近O(1),性能更高一些。
所以我们平常使用的各种Map或dictionary结构,大都是基于哈希表实现的。
从算法实现难度上来比较,skiplist比平衡树要简单得多。
四、合理的数据编码
对于每一种数据类型来说,底层的支持可能是多种数据结构,什么时候使用哪种数据结构,这就涉及到了编码转化的问题。
那我们就来看看,不同的数据类型是如何进行编码转化的:
- String:存储数字的话,采用int类型的编码,如果是非数字的话,采用 raw 编码;
- List:字符串长度及元素个数小于一定范围使用 ziplist 编码,任意条件不满足,则转化为 linkedlist 编码;
- Hash:hash 对象保存的键值对内的键和值字符串长度小于一定值及键值对;
- Set:保存元素为整数及元素个数小于一定范围使用 intset 编码,任意条件不满足,则使用 hashtable 编码;
- Zset:zset 对象中保存的元素个数小于及成员长度小于一定值使用 ziplist 编码,任意条件不满足,则使用 skiplist 编码。
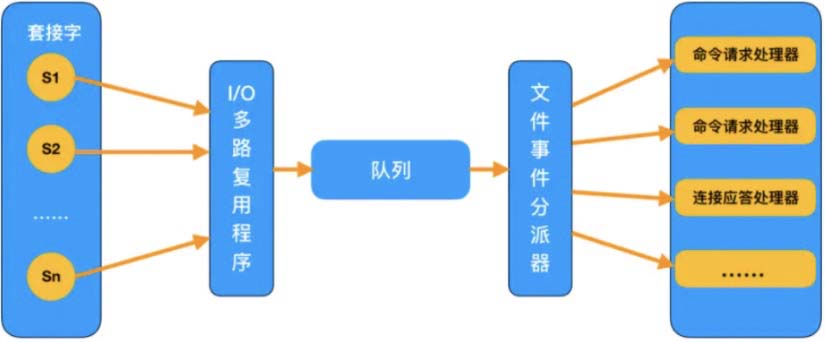
五、合适的线程模型

1. I/O多路复用模型
2. 避免上下文切换
3. 单线程模型
总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持好代码网。