这道数学题怎么做?
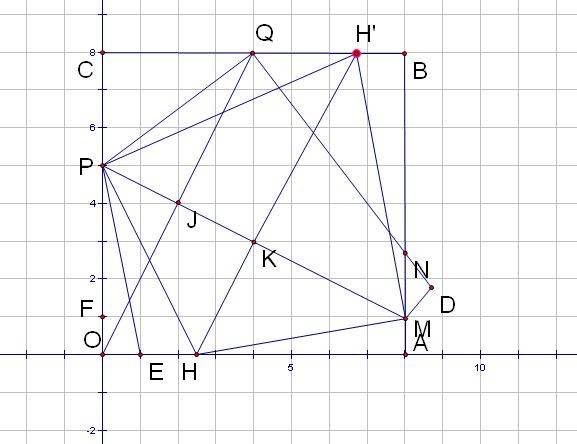
1:若点Q为线段BC边中点,求出点P.点M坐标。
2:在1的条件下。设△OEFP重叠面积为S,求S与t 的函数关系式;
3:在1的条件下,在正方形OABC边上,是否存在点H,使△PMH为等腰三角形,若存在,求出点H的坐标,若不存在,请说明理由;
4:若点Q为线段BC上的任一点(不与点B,C重合),△BNQ的周长是否发生变化,若不发生变化,若发生变化,说明理由。

2025-02-24 12:14:26
1、如图所示:连接OQ与PM相交与J,由POAM与QPMD对称,可知J为OQ中点,Q(4,8),故J(2,4),OQ与PM垂直,OQ斜率k=2,故PM斜率k=-0.5
所以PM方程为y=-0.5(x-2)+4,
所以P(0,5)M(8,1)
2、F点还没有过P点时△OEFP=△OEP,所以S=0.5*5*t=2.5t,t<=5
F点过P点时△OEFP=△OEF,所以S=0.5*t*t,8>=t>5
3两种情况
(1)PM为等腰三角形底边(x-0)^2+(y-5)^2=(8-x)^2+(1-y)^2
OA边:y=0,x=2.5,取(2.5,0)
AB边:x=8,y=11,无解
BC边:y=8,x=17/4,取(17/4,8)
CO边:x=0,y=-5,无解
(2)PM为等腰三角形侧边(x-0)^2+(y-5)^2=(8-0)^2+(1-5)^2=80或者(x-8)^2+(y-1)^2=(8-0)^2+(1-5)^2=80
OA边:针对方程1 y=0,x=sqr(55)或者-sqr(55),取(sqr(55),0);针对方程2无解
AB边:针对方程1 x=8,y=9或者1,无解;针对方程2无解
BC边:针对方程2 y=8,x=8+sqr(31)或者8-sqr(31),取(8-sqr(31),8);针对方程1 无解
CO边:针对方程1 x=0,y=5或者-3,无解;针对方程2无解
3、设Q(x0,8),J(x0/2,8/2),OQ与PM垂直,OQ斜率k=8/x0,故PM斜率k=-x0/8
所以PM方程为y=-x0/8(x-x0/2)+4
所以P(0,(x0^2+64)/8)
PQ斜率k=(64-x0^2)/16/x0,QN斜率k=16*x0/(x0^2-64)
QN方程y=16*x0/(x0^2-64)(x-x0)+8
故N(8,-(16*x0/(x0+8)+8))
△BNQ的周长L=?
只要细心做应该可以消掉x0
还有一种思路:从三角函数考虑,角MND=角QNB
2问是在一的条件下,设三角形OEF与四边形OAMP的重叠面积为S,求S与t的函数关系式
呵呵,问题没搞清楚,其实也简单啊
F点还没有过P点时重叠面积为△OEF的面积,所以S=0.5*t*t,t=t>5)
两者相较于(2t-10,10-t),四边形面积分为三部分,一个矩形,两个三角形
S=(2t-10)*(10-t)+0.5*(5-10+t)*(2t-10)+0.5*(10-t)*(10-t),8>=t>5
热门标签
