线性代数秩,证明r(A^T·A)=r(A)
最新回答

ら面具背后の殇う
2024-11-25 11:07:01
证明过程如图所示:

在一个m维
线性空间
E中,一个向量组的秩
表示的是其生成的子空间的维度。考虑m× n矩阵,将A的秩定义为向量组F的秩,则可以看到如此定义的A的秩就是矩阵 A的线性无关纵列的极大数目。即 A的列空间的维度(列空间是由 A的纵列生成的 F的子空间)。因为列秩和行秩是相等的,我们也可以定义 A的秩为 A的行空间的维度。
扩展资料
计算矩阵A的秩的最容易的方式是
高斯消去法
。高斯算法生成的 A的行梯阵形式有同 A一样的秩,它的秩就是非零行的数目。例如考虑4×4矩阵。
我们看到第 2 纵列是第 1 纵列的两倍,而第4纵列等于第1和第3纵列的总和。第1和第3纵列是线性无关的,所以A的秩是2。

浮华沧桑
2024-11-25 08:31:45
你好!可以利用齐次线性方程组的解的性质如图证明这个结论。经济数学团队帮你解答,请及时采纳。谢谢!


我们的未来
2024-11-25 10:19:25
简单分析一下,答案如图所示


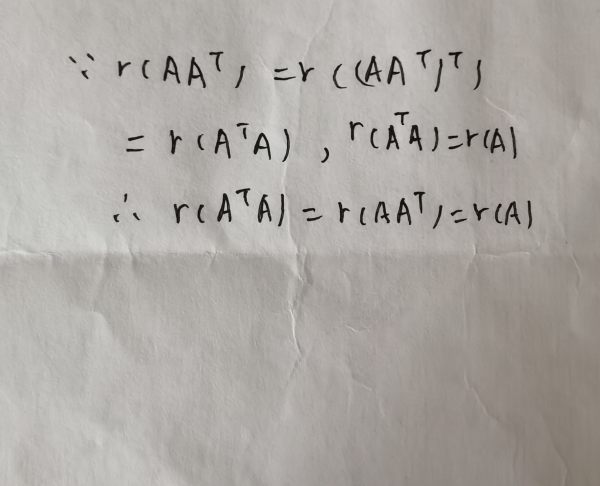
热门标签
