小学数学中的几种巧算
2024-11-08 01:14:38
数学,计算是基础,也是必备能力。计算能力的提高,计算技巧的掌握,不仅可以提高做题速度,也可以提高做题正确率。
随着数学竞赛的蓬勃发展,数值计算充满了活力,除了遵循四则混合运算的运算顺序外,破局部考虑、立整体分析,巧妙、灵活地运用定律和方法,对处理一些貌似复杂的计算题常常有事半功倍的效果,常见的巧算方法有以下十种。
一、凑整法
运算定律是巧算的支架,是巧算的理论依据,根据式题的特征,应用定律和性质“凑整”运算数据, 能使计算比较简便。
1、加法“凑整”。利用加法交换律、结合律“凑整”,例如:
4673+27689+5327+22311
=(4673+5327)+(27689+22311)
= 10000+50000
= 60000
2、减法 “凑整”。 利用减法性质“凑整”, 例如:
50-13-7
= 50-(13+7)
= 30
3、乘法 “凑整”。利用乘法交换律、结合律、分配律“凑整”,例如:
125×4×8×25×78
=(125×8)×(4×25)×78
= 1000×100×78
= 7800000
4、补充数“凑整”。末尾是一个或几个0的数,运算起来比较简便。若数末尾不是0,而是98、51等,我们可以用(100-2)、(50+1)等来代替,使运算变得比较简便、快速。一般地我们把100叫做98的“大约强数”,2叫做98的“补充数”;50叫做51的“大约弱数”,1叫做51的“补充数”。把一个数先写成它的大约强(弱)数与补充数的差(和),然后再进行运算,例如:
(1)387+99
=387+(100-1)
=387+100-1
=486
(2)1680-89
=1680-(100-11)
=1680-100+11
=1580+11
=1591
(3)69×101
=69×(100+1)
=6900+69
=6969
二、约分法
根据式题结构,采用约分,能使计算比较简便。例如:
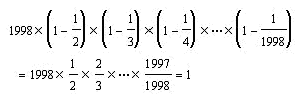
三、基数法
根据数据特征,从诸多数中选择一个做计算基础的数,通过“割”、“补”,采用“以乘代加”的方法速算。例如:
17+18+16+17+14+19+13+14
(解题时,可以选择17为基准数,以乘代加解答如下。)
=17×8+1-1-3+2-4-3
=17×8-8
=128
四、公式法
等差数列,是指每两个相邻的数之间差都相等的数列。等差数列求和,可以用公式:和=(首项+尾项)×项数÷2。例如:
13+14+15+16+17+18+19+20+21+22
=(13+22)×10÷2
=175
另外,如果加数的项数是奇数个,也可以直接用排列在正中间的数(中间项)乘以项数,去求它们的和。例如:
3+5+7+9+11+13+15+17+19
=11(中间项)×9(项数)
=99
五、变形法
恒等变形是一种重要的思想和方法,也是一种重要的解题技巧。它利用我们学过的知识,去进行有目的的数学变形,常常能使题目很快地获得解答。例如:
1、计算 9999×2222+3333×3334
(此题如果直接乘,数字较大,容易出错.如果将9999变为3333×3,规律就出现了.) 9999×2222+3333×3334
=3333×3×2222+3333×3334
=3333×6666+3333×3334
=3333×(6666+3334)
=3333×10000
=33330000
2、
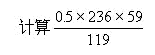
(将分子部分变形,可以使运算简便。)
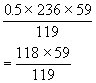
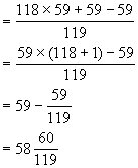
3、
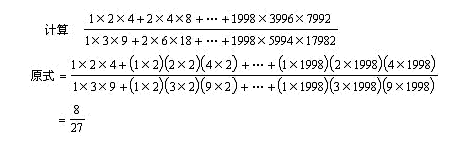
2024-11-08 01:12:12
我来答共1条回答
新野旁观者知道合伙人教育行家2018-06-01
数学,计算是基础,也是必备能力。计算能力的提高,计算技巧的掌握,不仅可以提高做题速度,也可以提高做题正确率。
随着数学竞赛的蓬勃发展,数值计算充满了活力,除了遵循四则混合运算的运算顺序外,破局部考虑、立整体分析,巧妙、灵活地运用定律和方法,对处理一些貌似复杂的计算题常常有事半功倍的效果,常见的巧算方法有以下十种。
一、凑整法
运算定律是巧算的支架,是巧算的理论依据,根据式题的特征,应用定律和性质“凑整”运算数据, 能使计算比较简便。
1、加法“凑整”。利用加法交换律、结合律“凑整”,例如:
4673+27689+5327+22311
=(4673+5327)+(27689+22311)
= 10000+50000
= 60000
2、减法 “凑整”。 利用减法性质“凑整”, 例如:
50-13-7
= 50-(13+7)
= 30
3、乘法 “凑整”。利用乘法交换律、结合律、分配律“凑整”,例如:
125×4×8×25×78
=(125×8)×(4×25)×78
= 1000×100×78
= 7800000
4、补充数“凑整”。末尾是一个或几个0的数,运算起来比较简便。若数末尾不是0,而是98、51等,我们可以用(100-2)、(50+1)等来代替,使运算变得比较简便、快速。一般地我们把100叫做98的“大约强数”,2叫做98的“补充数”;50叫做51的“大约弱数”,1叫做51的“补充数”。把一个数先写成它的大约强(弱)数与补充数的差(和),然后再进行运算,例如:
(1)387+99
=387+(100-1)
=387+100-1
=486
(2)1680-89
=1680-(100-11)
=1680-100+11
=1580+11
=1591
(3)69×101
=69×(100+1)
=6900+69
=6969
二、约分法
根据式题结构,采用约分,能使计算比较简便。例如:
三、基数法
根据数据特征,从诸多数中选择一个做计算基础的数,通过“割”、“补”,采用“以乘代加”的方法速算。例如:
17+18+16+17+14+19+13+14
(解题时,可以选择17为基准数,以乘代加解答如下。)
=17×8+1-1-3+2-4-3
=17×8-8
=128
四、公式法
等差数列,是指每两个相邻的数之间差都相等的数列。等差数列求和,可以用公式:和=(首项+尾项)×项数÷2。例如:
13+14+15+16+17+18+19+20+21+22
=(13+22)×10÷2
=175
另外,如果加数的项数是奇数个,也可以直接用排列在正中间的数(中间项)乘以项数,去求它们的和。例如:
3+5+7+9+11+13+15+17+19
=11(中间项)×9(项数)
=99
五、变形法
恒等变形是一种重要的思想和方法,也是一种重要的解题技巧。它利用我们学过的知识,去进行有目的的数学变形,常常能使题目很快地获得解答。例如:
1、计算 9999×2222+3333×3334
(此题如果直接乘,数字较大,容易出错.如果将9999变为3333×3,规律就出现了.) 9999×2222+3333×3334
=3333×3×2222+3333×3334
=3333×6666+3333×3334
=3333×(6666+3334)
=3333×10000
=33330000
2、
(将分子部分变形,可以使运算简便。)
热门标签
