兄弟们帮我讲解下,大学线性代数题目求解: 设A,B为三阶方阵,E为单位矩阵,并且有A2+2AB+2B-E=0,若已知?
大学线性代数题目求解: 设A,B为三阶方阵,E为单位矩阵,并且有A2+2AB+2B-E=0,若已知A=(2 0 1 .0 2 0 .1 0 3)求方阵B大学线性代数题目求解: 设A,B为三阶方阵,E为单位矩阵,并且有A2+2AB+2B-E=0,若已知
最新回答

失意的片刻
2024-10-16 11:40:16
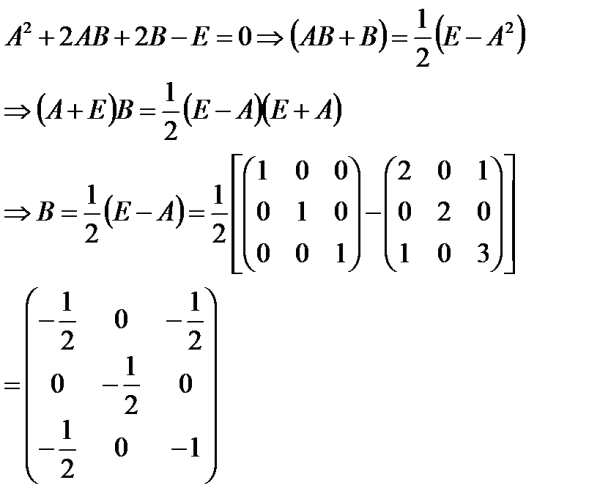
提供方法,不保证结果无误。
追问
可是(E+A)(E-A)不是E2-A2吗 题目是E-A2啊
而且A+E=E+A 这个不用证明吗
追答
E^2=E. 矩阵加大满足交换律,不必证明。
E^2=E. 矩阵加法满足交换律,不必证明。
热门标签
