Matlab求大神帮忙啦……这个题不会做……怎么设计程序……我是小白

几天前就编好了程序，一直没顾上上传。

（1）求猎狗最小速度的问题：

理论分析请参考下述文献：钱杏芳，导弹飞行力学，北理工出版社，2000.8
p97，式4-11
追踪法，从开始到命中目标所需时间为
     tk = r0 ( p + cos(q0) ) / ( ( p^-1 ) * Vt )
取基准线平行于兔子运动方向，则q0=-pi/2，cos(q0）=0，所以
     tk = r0/Vt * p/(p^2-1)
所需最小速度即为，兔子刚好在tk时间内跑到A点，即求解下面的方程：

     s = r0 * p/(p^2-1)

其中s=120为OA长度，r0=200为OB长度。解出p（注意取正数解）再乘以兔子速度即可。

r0 = 200;
Vt = 8;
% 兔子移动的距离
s = 120;
% （1）猎狗最小速度
% 钱杏芳，导弹飞行力学，北理工出版社，2000.8
% p97，式4-11
% 追踪法，从开始到命中目标所需时间为
%     tk = r0 ( p + cos(q0) ) / ( ( p^-1 ) * Vt )
% 取基准线平行于兔子运动方向，则q0=-pi/2，cos(q0）=0，所以
%     tk = r0/Vt * p/(p^2-1)
syms p
p = solve( s - r0 * p/(p^2-1) );
p = double(p);
p = p(p>=0);
V = Vt * p

答案为

V =
   17.0803

（2）猎狗跑过的时间和路程

由上一步的结果很容易求出：

tk = r0/Vt * p/(p^2-1)
S = V * tk

答案为

tk =
   15.0000
S =
  256.2050

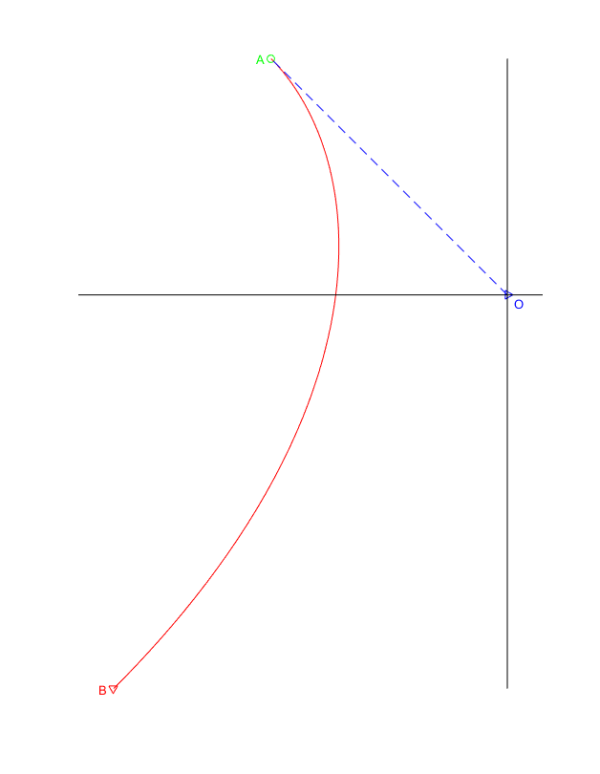
（3）画出猎狗奔跑的曲线图

可以用ode45求解，需要注意适当减小求解器的误差控制参数RelTol和AbsTol。

代码在下一步统一给出。

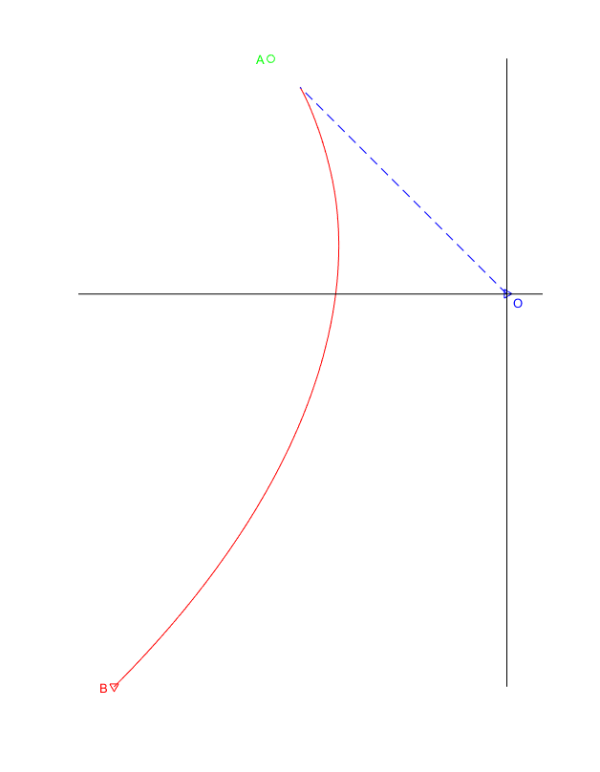
（4）这一步的要求已经很难通过理论分析来做了。

可以用数值方法解微分方程，但所涉及的问题对于一般的初学者应该是比较难以处理的。

我把主要涉及的问题尽量提到，但不会详细讲解。题主既自称“小白”，就请不要就这个问题问太多了，否则展开讲太繁琐了。

主要涉及到的问题：

a、速度是变化的，需要把两个速度也作为状态变量，相应增加两个微分方程。

b、需要设置结束事件，让猎狗追到兔子后就停止仿真。

c、此处特别需要减小求解器的误差控制参数RelTol和AbsTol，否则在猎狗接近兔子时，相对方位几乎成了随机数，最后的一段时间差不多在做布朗运动了。

d、程序采用嵌套函数的结构，以方便函数间共享几个相关的变量。

参考代码：

function dog_chase_rabbit
r0 = 200;
Vt = 8;
% 兔子移动的距离
s = 120;

% （1）猎狗最小速度
syms p
p = solve( s - r0 * p/(p^2-1) );
p = double(p);
p = p(p>=0);
V = Vt * p

% （2）猎狗跑过的时间和路程
tk = r0/Vt * p/(p^2-1)
S = V * tk

% （3）曲线图
psi1 = pi / 4;
psi2 = pi * 3 / 4;
X0 = [r0*cos(psi1+pi); r0*sin(psi1+pi); 0; 0];
opt = odeset('reltol',1e-6,'abstol',1e-7);
[t,X] = ode45(@chase, [0 tk], X0,opt);
plot_res(1)

    function dX = chase(t, X)
        % X(1,2) - x1 y1
        x1 = X(1); y1 = X(2);
        x2 = X(3); y2 = X(4);
        Q = atan2(y2-y1, x2-x1);
        dX = [ ...
            V * cos(Q); V * sin(Q); ...
            Vt * cos(psi2); Vt * sin(psi2) ...
            ];
    end

    function plot_res(i)
        figure(i)
        clf
        hold on
        plot(s*cos(psi2),s*sin(psi2),'go')
        text(s*cos(psi2),s*sin(psi2),'A  ','Horiz','right','color','g')
        plot(X0(1),X0(2),'rv')
        text(X0(1),X0(2),'B  ','Horiz','right','color','r')
        plot(X0(3),X0(4),'b>')
        text(X0(3),X0(4),'  O','Horiz','left','Vert','top','color','b')
        plot(X(:,1),X(:,2),'r-',X(:,3),X(:,4),'b--')
        axis equal off
        plot([0 0],ylim,'k')
        plot(xlim,[0 0],'k')
    end

% （4）如果距离为30米时，兔子速度每秒减半，猎狗速度每秒增加1.1倍
%     此时应考虑把两个速度也作为状态变量，并且设置结束事件
X0 = [r0*cos(psi1+pi); r0*sin(psi1+pi); 0; 0; V; Vt];
opt = odeset('reltol',1e-6,'abstol',1e-7,'Events',@events);
[t,X] = ode45(@chase2, [0 tk], X0,opt);
plot_res(2)
S = sum(sqrt(diff(X(:,1)).^2+diff(X(:,2)).^2))
tk = t(end)

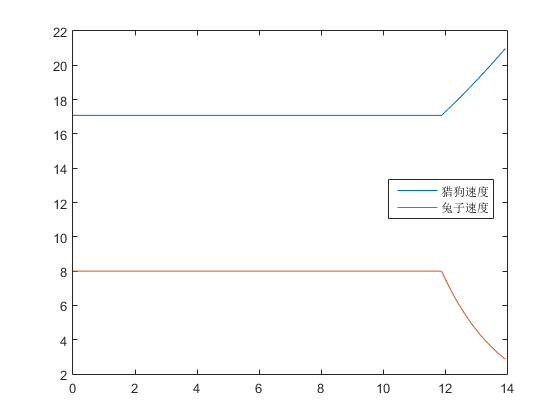
figure(3)
plot(t,X(:,5:6))
legend('猎狗速度','兔子速度',0)

    function dX = chase2(t, X)
        % 提取状态变量
        x1 = X(1); y1 = X(2);
        x2 = X(3); y2 = X(4);
        V = X(5); Vt = X(6);
        Q = atan2(y2-y1, x2-x1);
        % 考虑速度变化
        d = sqrt((x2-x1)^2+(y2-y1)^2);
        dV = 0.1 * V * (d <= 30);
        dVt = -0.5 * Vt * (d <= 30);
        % 微分方程
        dX = [ ...
            V * cos(Q); V * sin(Q); ...
            Vt * cos(psi2); Vt * sin(psi2); ...
            dV; dVt ...
            ];
    end
    function [value,isterminal,direction] = events(t,X)
        % 距离小于0.001时结束仿真
        value = sqrt((X(3)-X(1))^2+(X(4)-X(2))^2) - 1e-3;
        isterminal = 1;
        direction = -1;
    end
end