如何用泰勒公式“展开”三角函数
最新回答

天空暗下来我就是光
2024-09-21 00:38:16
sin x 可以如何 “ 展开 ”?写成式子就是:
最后以省略号结束,代表 “ 无穷 ”,需要求的就是 a0,a1,a2,…… 的值,准确地说就是通项公式。然后,我们就可以开始 “ 微分 ” 了,就是等式两边同时、不停地微分下去。左边的三角函数的微分,其实是四个一循环的:sin x ➜ cos x ➜ - sin x ➜ - cos x,再回到 sin x……我们也会注意到,凡是把右边微分后,第一项(常数)就为 0 了,也就是可以直接忽略。

这样一来,等式左边在有规律地循环着,等式右边每次都减少一项。当然,x = 0 时等式也会成立,那将 x = 0 带入,将消去所有 x 指数大于 0 的项(都是 0 啊)。这样一来,就可以顺利求出 a0,a1,a2,……啦,sin 0、cos 0、- sin 0 和 - cos x 分别是 0、+1 、0、-1(显然的规律)。上面是微分的过程,下面是对于所有系数得到的等式。
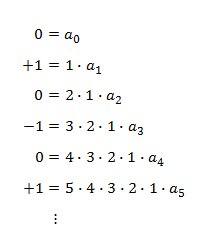
最后,等式左边是四个一循环,可以从除以 4 的余数来考虑(分类);然后,等是右边可以用字母来代替,就是 k! × ak,这里 k! 代表阶乘。所以说,我们可以得到一个看上去漂亮的结果:

如果将系数数列 a 代入,那么偶数项都会消掉(系数为 0),只剩下一加一减的奇数项了。这就是泰勒展开(其实泰勒展开有好几个,这里只是 sin x 的泰勒展开):
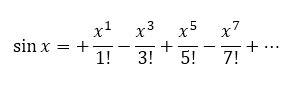

睫毛下的眼泪坠落花已枯萎
2024-09-21 00:29:11
1. 正弦函数的泰勒展开式:
\[ \sin(x) = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \cdots = \sum_{n=0}^{\infty} (-1)^n \dfrac{x^{2n+1}}{(2n+1)!} \]
2. 余弦函数的泰勒展开式:
\[ \cos(x) = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \cdots = \sum_{n=0}^{\infty} (-1)^n \dfrac{x^{2n}}{(2n)!} \]
在实际计算中,可以根据需要选择展开的阶数来逼近所需的精度。通常,展开到几阶就足以得到满意的近似值。这些泰勒展开式可用于计算三角函数的近似值,特别是在无法直接计算的情况下。
热门标签
