计算二重积分I= ∫∫根号下1-x^2-y^2 dxdy 其中D: x^2+y^2<=1 x>=0 y>=0 (∫∫符号下为D) 要详解
最新回答

雪鬓
2024-09-18 00:10:44
令x=pcosa,y=psina
a∈[0,π/2]
p∈[0,1]代入得
原积分=∫[0,π/2]∫[0,1]√(1-p^2)*pdpda
=∫[0,π/2]da∫[0,1]√(1-p^2)*pdp
=π/2*(-1/2)∫[0,1]√(1-p^2)d(1-p^2)
=π/2*(-1/3)(1-p^2)^(3/2)[0,1]
=π/6
追问
=π/2*(-1/2)∫[0,1]√(1-p^2)d(1-p^2)
=π/2*(-1/3)(1-p^2)^(3/2)[0,1]
这两步 没太看懂
追答
我晕啊,前一个直接积分,后一个是凑积分呀

一袭水袖舞倾城
2024-09-18 00:18:39
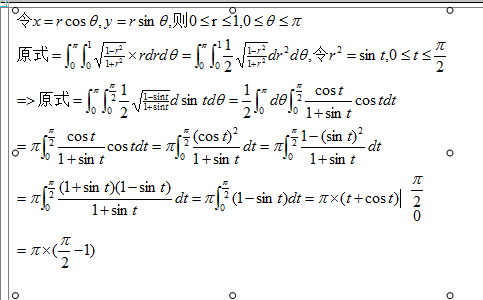
热门标签
