高中数学题,急求大神解答,要详细过程,谢谢…(图上5.6两题)
最新回答

只想待在家
2024-08-16 20:13:22
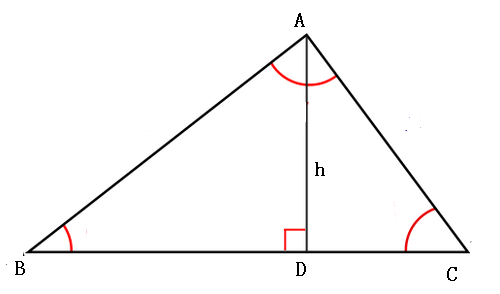
5、直角三角形,选A。如图,bcosC+ccosB=b*DC/b+c*BD/c=DC+BD=a=asinA
sinA=1,A=90度。
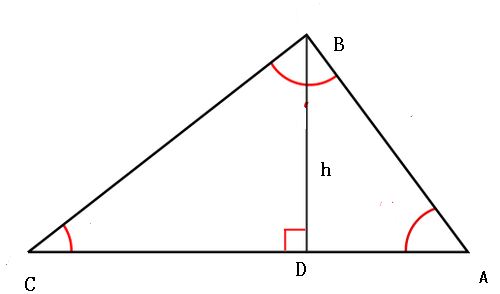
6、等腰三角形。b/(a-b)=sin2C/(sinA-sin2C)
bsinA=asin2C
∴结合正弦定理,有:sinBsinA=sinAsin2C。
显然,在△ABC中,有:sinA>0,∴simB=sin2C,∴B=2C,或B=180°-2C。
一、当B=2C时,
考虑到π/3<C<π/2,即:60°<C<90°,∴180°<3C<270°,∴-270°<-3C<-180°,
∴-90°<180°-3C<0°。
而A=180°-B-C=180°-3C,∴-90°<A<0°。这自然是不合理的,∴这种情况应舍去。
二、当B=180°-2C时,
A=180°-B-C=180°-(180°-2C)-C=C。
∴△ABC是以AC为底边的等腰三角形。
综上所述,得:△ABC是以AC为底边的等腰三角形。
热门标签
