spss软件怎么用?
最新回答
爱在天气晴
2024-07-27 00:40:59
旧事酒浓
2024-07-27 06:26:03
ぃ伊丽莎白鼠
2024-07-27 02:17:04
巅峰小学生
2024-07-27 02:09:34
如果想要自学spss软件,推荐使用在线数据分析平台SPSSAU。轻松好上手,分析操作全部均为三步,“拖拽点一下”即完成分析。
数据结果可以参考如下图:
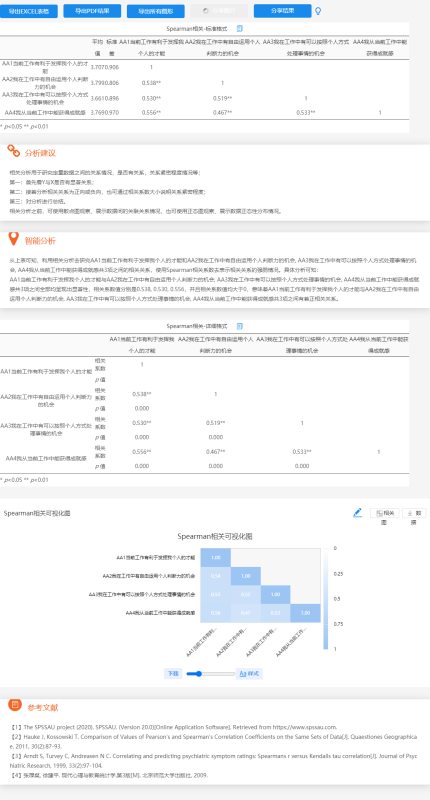
惊蛰花压重门
2024-07-27 08:13:52
热门标签
