二进制转换十进制的简单方法?
最新回答
逆风の蒲公英
2024-06-05 00:51:00
方法一:从右到左用二进制的每个数去乘以2的相应次方,小数点后则是从左往右
例:二进制数1101.01转化成十进制
1101.01(2)
=1*2【0】+0*2【1】+1*2【2】+1*2【3】 +0*2【-1】+1*2【-2】
=1+0+4+8+0+0.25=13.25(10)
方法二:把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。这种做法称为"按权相加"法。
对于有n位整数,m位小数的二进制数用加权系数展开式表示,可写为:N(2)=an-1×2n-1+an-2×2n-2+??+a1×21+a0×20+a-1×2-1+a-2×2-2+??+a-m×2-m(10)式中aj表示第j位的系数,它为0和1中的某一个数。
例:二进制数1101转化成十进制
1101(2)
=1*2【3】+1*2【2】+0*2【1】+1*2【0】
=13(10)
注意:
1、【】括号内数字代表次方,如【2】为二次方,【-1】为负一次方。
2、()括号内代表进制数,(2)为二进制,(10)为十进制。
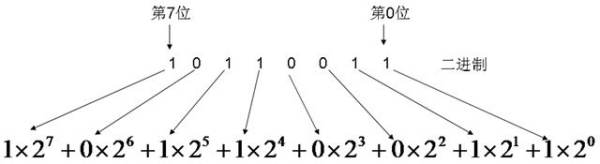
扩展资料:
以下为二进制转是进制代码:
int readint(int a) //a 是传入二进制位数
{
int sum = 0;
while (a--) {
sum *=2;
sum += getchar() - '0'; // getchar 读入相应十进制的每一位
}
return sum; // sum 是相应的十进制
}
参考资料来源:
百度百科-十进制转二进制
热门标签
