A是n阶矩阵,证明A有n个线性无关的特征向量时, A可对角化。求大神讲的明白一点~
最新回答

Mentos曼妥思
2024-05-19 10:30:50
n阶矩阵A相似于
对角矩阵
的充要条件是A有n个线性无关的特征向量。证明过程:
(1)必要性
设有可逆矩阵P,使得
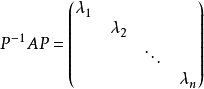
令矩阵P的n个
列向量
为则有
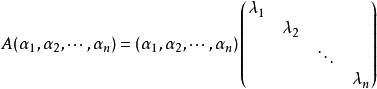
因而
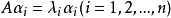
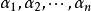
为线性无关的非零向量,它们分别是矩阵A对应于
特征值

(2)充分性。
由必要性的证明可见,如果矩阵A有n个线性无关的特征向量,设它们为
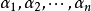
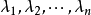
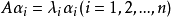
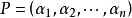

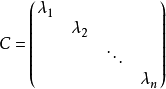
即
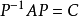
推论
若n阶矩阵A有n个不同的特征值,则A必能相似于对角矩阵。
说明:当A的
特征方程
有重根时.就不一定有n个线性无关的特征向量,从而未必能对角化。扩展资料
对角矩阵(diagonal matrix)是一个主
对角线
之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为
数量矩阵
;对角线上元素全为1的对角矩阵称为单位矩阵
。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。

香草天空
2024-05-19 09:12:13
则Ax1 =s1 x1, Ax2=s2x2 ..., Axn = snxn
或A(x1,x2,...,xn) = (x1,x2,...,xn)diag (s1, s2,...,sn)
diag(s1, s2,...,sn)表示(s1, s2,...,sn)为对角元素的方阵
因为x1,x2,...,xn线性无关,所以矩阵(x1,x2,...,xn)满秩可逆
所以
(x1,x2,...,xn)'A(x1,x2,...,xn) = diag(s1,s2,...sn)
其中(x1,x2,...,xn)'为(x1,x2,...,xn)的逆矩阵
热门标签
