两道初三的数学题,关于圆和相似的
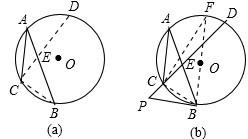
(1)试在AB上确定是否存在一点E,使AC²=AE·AB,并说明理由:
(2)在(1)的论证下,延长EC至点P,延长CE与圆O交于点D,连接PB,使PB=PE,如图(2),判断PB与圆O得位置关系,并说明理由。
2. 如图,点A在⊙O上,⊙A交⊙O于点B.C,点E是⊙O上任意一点,AE交BC于D,交⊙A于F。(1)AF²=AD·AE成立吗?理由
(2)BE·CE=DE·AE成立吗?理由
(3)点F是△BCE的内心吗?理由。
(4)若圆O得半径为3,圆A得半径为2,当点E运动到圆O得什么位置时,能使DE=8AD?理由
最新回答

哥特式·浅唱
2024-05-03 00:31:39
证明:因为AC²=AE·AB,角CAB是公共角,所以三角形ACB相似三角形AEC,所以角ACB=角CBA,所以A是中点。
(2)连接OA OB
角ACD+角CAB+BAO=90°
角ACD+角CAB=角CEB=角PBA 角BAO=ABO
所以角PBA+角ABO=90°
所以PB于园o相切
2. (1)连接AB OA
OA垂直平分BC,所以角AEB=角AEC
在圆O中,AEC=角CBA
所以角AEB=角CBA
角CBA=CBA
所以三角形ABE相似三角形ADB
即AB/AD=AE/AB
因为AF=AB
所以AF²=AD·AE
(2)成立
连接AC
由1得角AEB=角AEC
角EBA=角EAC
所以三角形AEC相似三角形BDE
所以BE·CE=DE·AE
(3) 连接AC BF
角EAC=角EBC
角FBC=1/2角FAC
所以角EBF=角CBF
因为角BEF=角CEF
所以F是中心
(4)

真相是假
2024-05-03 14:50:35
考点:切线的判定;圆周角定理;相似三角形的判定与性质.
专题:几何综合题.
分析:(1)使AC2=AE•AB成立,则应有△AEC∽△ACB,则应有∠B=∠ACE,则应有∠B对的弧与∠ACE对的弧相等,即点A是CAD的中点;
(2)过点B作直径BF,连接CF,根据圆周角定理及已知可得到∠PBCF=90°,OB是圆O的半径,从而得到PB是圆O的切线.
解答:解:(1)在优弧AB上截取弧AD=弧AC,则有∠B=∠ACD,
∵A=∠A,
∴△AEC∽△ACB.
∴AC:AB=AE:AC.
即AC2=AE•AB.
(2)如图b,过点B作直径BF,连接CF,
∵PB=PE,
∴∠PEB=∠PBE.
∵∠PEB=∠A+∠ACD,∠PBE=∠PBC+∠CBE,∠ACD=∠CBA=∠CBE,
∴∠A=∠PBC.
∵BF是直径,
∴∠BCF=-90°.
∵∠A=∠F,∠F+∠CBF=90°,
∴∠PBC+∠CBF=90°.
∵OB是圆O的半径,
∴PB是圆O的切线.
还行吗?
∵BF是直径,
∴∠BCF=-90°.
∵∠A=∠F,∠F+∠CBF=90°,
∴∠PBC+∠CBF=90°.
∵OB是圆O的半径,
∴PB是圆O的切线.

给十年后的我
2024-05-03 09:24:46
(2)相切
2
热门标签
