区块链密码算法是怎样的？

区块链作为新兴技术受到越来越广泛的关注，是一种传统技术在互联网时代下的新的应用，这其中包括分布式数据存储技术、共识机制和密码学等。随着各种区块链研究联盟的创建，相关研究得到了越来越多的资金和人员支持。区块链使用的Hash算法、零知识证明、环签名等密码算法:

Hash算法

哈希算法作为区块链基础技术，Hash函数的本质是将任意长度（有限）的一组数据映射到一组已定义长度的数据流中。若此函数同时满足：

（1）对任意输入的一组数据Hash值的计算都特别简单；

（2）想要找到2个不同的拥有相同Hash值的数据是计算困难的。

满足上述两条性质的Hash函数也被称为加密Hash函数，不引起矛盾的情况下，Hash函数通常指的是加密Hash函数。对于Hash函数，找到使得被称为一次碰撞。当前流行的Hash函数有MD5,SHA1,SHA2,SHA3。

比特币使用的是SHA256，大多区块链系统使用的都是SHA256算法。所以这里先介绍一下SHA256。

1、 SHA256算法步骤

STEP1：附加填充比特。对报文进行填充使报文长度与448模512同余（长度=448mod512），填充的比特数范围是1到512，填充比特串的最高位为1，其余位为0。

STEP2：附加长度值。将用64-bit表示的初始报文（填充前）的位长度附加在步骤1的结果后（低位字节优先）。

STEP3：初始化缓存。使用一个256-bit的缓存来存放该散列函数的中间及最终结果。

STEP4：处理512-bit（16个字）报文分组序列。该算法使用了六种基本逻辑函数，由64 步迭代运算组成。每步都以256-bit缓存值为输入，然后更新缓存内容。每步使用一个32-bit 常数值Kt和一个32-bit Wt。其中Wt是分组之后的报文，t=1,2,...,16 。

STEP5：所有的512-bit分组处理完毕后，对于SHA256算法最后一个分组产生的输出便是256-bit的报文。

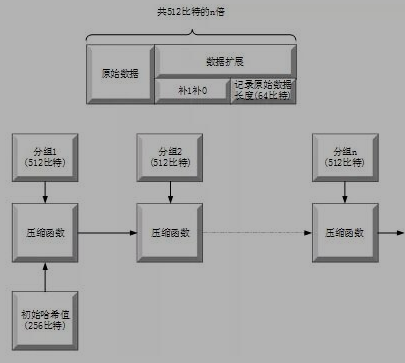
作为加密及签名体系的核心算法，哈希函数的安全性事关整个区块链体系的底层安全性。所以关注哈希函数的研究现状是很有必要的。

2、 Hash函的研究现状

2004年我国密码学家王小云在国际密码讨论年会（CRYPTO）上展示了MD5算法的碰撞并给出了第一个实例（Collisions for hash functions MD4, MD5, HAVAL-128 and RIPEMD，rump session of CRYPTO 2004，How to Break MD5 and Other Hash Functions，EuroCrypt 2005）。该攻击复杂度很低，在普通计算机上只需要几秒钟的时间。2005年王小云教授与其同事又提出了对SHA-1算法的碰撞算法，不过计算复杂度为2的63次方，在实际情况下难以实现。

2017年2月23日谷歌安全博客上发布了世界上第一例公开的SHA-1哈希碰撞实例，在经过两年的联合研究和花费了巨大的计算机时间之后，研究人员在他们的研究网站SHAttered上给出了两个内容不同，但是具有相同SHA-1消息摘要的PDF文件，这就意味着在理论研究长期以来警示SHA-1算法存在风险之后，SHA-1算法的实际攻击案例也浮出水面，同时也标志着SHA-1算法终于走向了生命的末期。

NIST于2007年正式宣布在全球范围内征集新的下一代密码Hash算法，举行SHA-3竞赛。新的Hash算法将被称为SHA-3，并且作为新的安全Hash标准，增强现有的FIPS 180-2标准。算法提交已于2008年10月结束，NIST 分别于2009年和2010年举行2轮会议，通过2轮的筛选选出进入最终轮的算法，最后将在2012年公布获胜算法。公开竞赛的整个进程仿照高级加密标准AES 的征集过程。2012年10月2日，Keccak被选为NIST竞赛的胜利者，成为SHA-3。

Keccak算法是SHA-3的候选人在2008年10月提交。Keccak采用了创新的的“海绵引擎”散列消息文本。它设计简单，方便硬件实现。Keccak已可以抵御最小的复杂度为2n的攻击，其中N为散列的大小。它具有广泛的安全边际。目前为止，第三方密码分析已经显示出Keccak没有严重的弱点。

KangarooTwelve算法是最近提出的Keccak变种，其计算轮次已经减少到了12，但与原算法比起来，其功能没有调整。

零知识证明

在密码学中零知识证明（zero-knowledge proof, ZKP）是一种一方用于向另一方证明自己知晓某个消息x，而不透露其他任何和x有关的内容的策略，其中前者称为证明者（Prover），后者称为验证者（Verifier）。设想一种场景， 在一个系统中， 所有用户都拥有各自全部文件的备份， 并利用各自的私钥进行加密后在系统内公开。 假设在某个时刻，用户Alice希望提供给用户Bob她的一部分文件，这时候出现的问题是Alice如何让Bob相信她确实发送了正确的文件。一个简单地处理办法是Alice将自己的私钥发给Bob，而这正是 Alice不希望选择的策略，因为这样 Bob可以轻易地获取到Alice的全部文件内容。零知识证明便是可以用于解决上述问题的一种方案。零知识证明主要基于复杂度理论，并且在密码学中有广泛的理论延伸。在复杂度理论中，我们主要讨论哪些语言可以进行零知识证明应用，而在密码学中，我们主要讨论如何构造各种类型的零知识证明方案，并使得其足够优秀和高效。

 环签名群签名

1、群签名

在一个群签名方案中，一个群体中的任意一个成员可以以匿名的方式代表整个群体对消息进行签名。与其他数字签名一样，群签名是可以公开验证的，且可以只用单个群公钥来验证。群签名一般流程：

（1）初始化，群管理者建立群资源，生成对应的群公钥（Group Public Key）和群私钥（Group Private Key）群公钥对整个系统中的所有用户公开，比如群成员、验证者等。

（2）成员加入，在用户加入群的时候，群管理者颁发群证书（Group Certificate）给群成员。

（3）签名，群成员利用获得的群证书签署文件，生成群签名。

（4）验证，同时验证者利用群公钥仅可以验证所得群签名的正确性，但不能确定群中的正式签署者。

（5）公开，群管理者利用群私钥可以对群用户生成的群签名进行追踪，并暴露签署者身份。

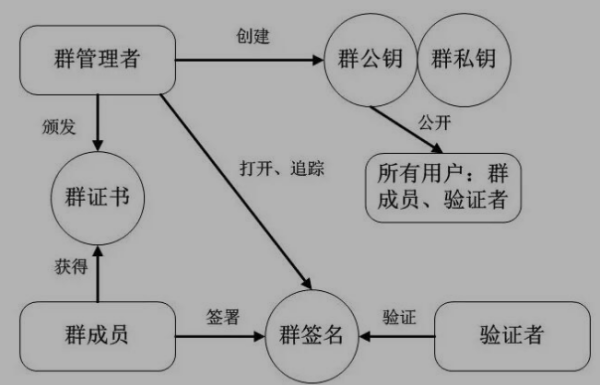
2、环签名

2001年，Rivest, shamir和Tauman三位密码学家首次提出了环签名。是一种简化的群签名，只有环成员没有管理者，不需要环成员间的合作。环签名方案中签名者首先选定一个临时的签名者集合,集合中包括签名者。然后签名者利用自己的私钥和签名集合中其他人的公钥就可以独立的产生签名,而无需他人的帮助。签名者集合中的成员可能并不知道自己被包含在其中。

环签名方案由以下几部分构成：

（1）密钥生成。为环中每个成员产生一个密钥对(公钥PKi,私钥SKi)。

（2）签名。签名者用自己的私钥和任意n个环成员(包括自己)的公钥为消息m生成签名a。

（3）签名验证。验证者根据环签名和消息m,验证签名是否为环中成员所签,如果有效就接收,否则丢弃。

环签名满足的性质：

（1）无条件匿名性:攻击者无法确定签名是由环中哪个成员生成,即使在获得环成员私钥的情况下,概率也不超过1/n。

（2）正确性:签名必需能被所有其他人验证。

（3）不可伪造性:环中其他成员不能伪造真实签名者签名,外部攻击者即使在获得某个有效环签名的基础上,也不能为消息m伪造一个签名。

3、环签名和群签名的比较

（1）匿名性。都是一种个体代表群体签名的体制，验证者能验证签名为群体中某个成员所签，但并不能知道为哪个成员，以达到签名者匿名的作用。

（2）可追踪性。群签名中，群管理员的存在保证了签名的可追踪性。群管理员可以撤销签名，揭露真正的签名者。环签名本身无法揭示签名者,除非签名者本身想暴露或者在签名中添加额外的信息。提出了一个可验证的环签名方案,方案中真实签名者希望验证者知道自己的身份,此时真实签名者可以通过透露自己掌握的秘密信息来证实自己的身份。

（3）管理系统。群签名由群管理员管理，环签名不需要管理，签名者只有选择一个可能的签名者集合，获得其公钥，然后公布这个集合即可，所有成员平等。

链乔教育在线旗下学硕创新区块链技术工作站是中国教育部学校规划建设发展中心开展的“智慧学习工场2020-学硕创新工作站 ”唯一获准的“区块链技术专业”试点工作站。专业站立足为学生提供多样化成长路径，推进专业学位研究生产学研结合培养模式改革，构建应用型、复合型人才培养体系。