r语言如何求矩阵中某一列的总和

2024-09-29 06:49:35
设矩阵为A
方法一:colSums(A)
方法二:apply(A,2,sum)
> x<-matrix(c(1,1,2,1,2,3,4,1),4,2)
> x
[,1] [,2]
[1,] 1 2
[2,] 1 3
[3,] 2 4
[4,] 1 1
> length(which((x[,1]==1)))
[1] 3
> length(which((x[,2]==1)))
[1] 1
#x[,1]==1判断是否为1,返回True或False
# which((x[,1]==1))返回为True的行号
#length(which((x[,1]==1)))返回为True的行数,即1的个数
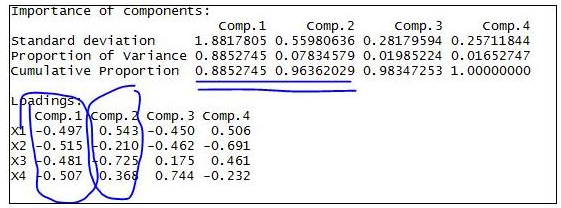
简正模式
矩阵在物理学中的另一类泛应用是描述线性耦合调和系统。这类系统的运动方程可以用矩阵的形式来表示,即用一个质量矩阵乘以一个广义速度来给出运动项,用力矩阵乘以位移向量来刻画相互作用。求系统的解的最优方法是将矩阵的
以上内容参考:

2024-09-29 05:16:50
第一步,声明矩阵t,利用矩阵函数matrix,nrow为5,ncol为5,并打印矩阵t,如下图所示:

第二步,获取矩阵t第四列数据,可以直接使用t[,4],这样可以获取到第四列数据,如下图所示:

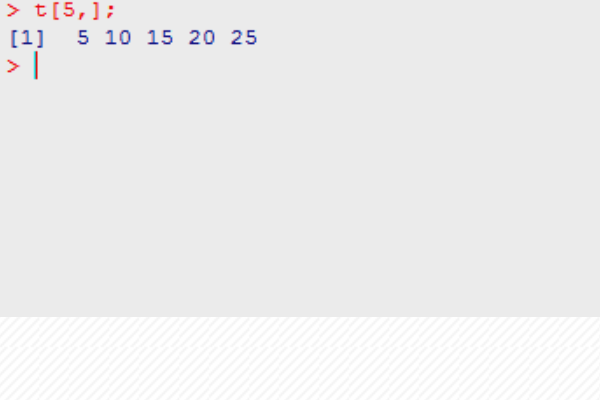
第三步,如果想要获取第五列数据,可以使用t[5,],如下图所示:
第四步,如果想要获取第三行和第四列交叉点的数据,使用t[3,4],如下图所示:

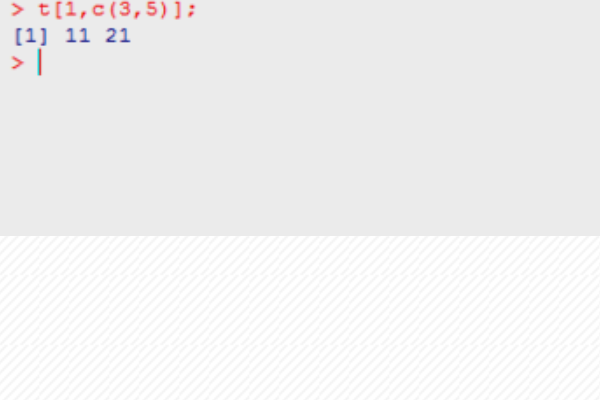
第五步,获取某一行的一列或两列以上的数据,使用t[1,c(3,5)],表示获取第一行和第三行、第五个交叉点的数据,如下图所示:
第六步,如果想要获取第二行、第三行和第二列的数据,利用t[c(2,3),2],如下图所示:


2024-09-29 02:34:56
方法一、
colSums(A)
方法二、
apply(A,2,sum)

2024-09-29 07:04:45
热门标签
