C语言编程，已知三角形的三边长a,b,c，计算求三角形面积的公式为：
要求编写程序，从键盘输入a,b,c的值，计算并输出三角形的面积。
[提示：程序运行时应保证输入的a,b,c值满足三角形成立的条件，这样计算得到的三角形面积才有意义。另外，将面积计算的数学公式写成合法的C语言表达式如下：
area = sqrt(s*(s-a)*(s-b)*(s-c))
注意写成：
area = sqrt(s(s-a)(s-b)(s-c))
是不错误的。
将数学公式 = ,写成如下C语言表达式：
s = 0.5*(a+b+c)
最新回答
浓烈往事
2024-04-25 01:22:57
程序代码如下：
#include <stdio.h>
#include <math.h>
int main()
{
printf("输入三个边长:\n");
float a,b,c;
float s,area;
scanf("%f%f%f",&a,&b,&c);
s = (a+b+c)/2;
area = sqrt(s*(s-a)*(s-b)*(s-c));
if(a+b>c && b+c>a && a+c>b)
printf("面积是%.2f\n",area);
else
printf("三条边无法构成三角形");
return 0;
}
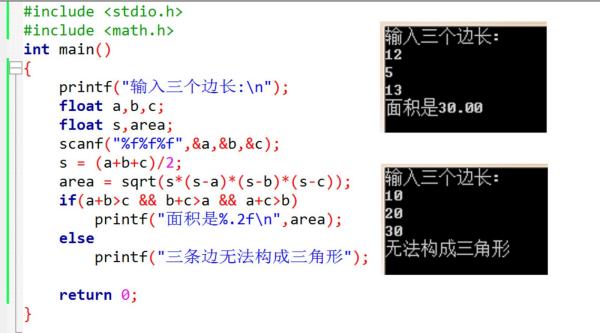
扩展资料：
三角形具有以下性质：
1、三角形任意两边之和大于第三边，任意两边之差小于第三边。
2、在平面上三角形的内角和等于180°（内角和定理）。
3、在平面上三角形的外角和等于360° (外角和定理)。
4、三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点。
5、三角形的任意一条中线将这个三角形分为两个面积相等的三角形。
参考资料：
百度百科-三角形面积公式
百度百科-三角形性质
琉璃水色
2024-04-25 00:52:36
一、程序代码如下：
{
#include <stdio.h>
#include <math.h>
int main()
{
printf("请分别输入三角形边长，按回车:\n");
float a,b,c;
float s,area;
scanf("%f%f%f",&a,&b,&c);
if(a+b>c && a+c>b && b+c>a) //判断是否可以构成三角形。
{
s=(a+b+c)/2;//计算半周长
area=sqrt(s*(s-a)*(s-b)*(s-c));//套用海伦公式，计算面积
printf("这个三角形的面积为%lf\n", area);//输出结果
}
else printf("无法构成三角形\n");//输入不合法，提示。
return 0;
}
二、将程序生产EXE文件后运行，或点击下图三角运行进行测试，如果程序编写正确，会弹出命令窗口。
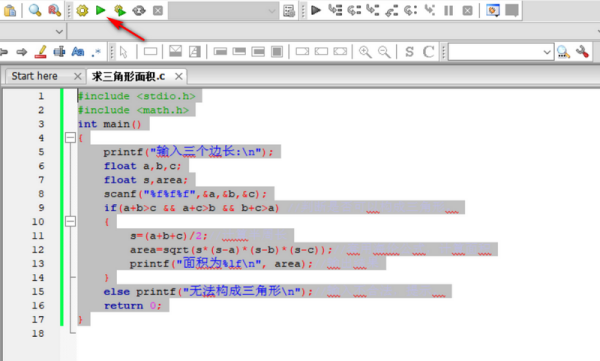
三、窗口显示“输入三个边长”，这时就可以输入三个边长的数据了，输入一个边长，按回车输入下个一个边长，如果输入正确是三角形边长数据，显示三角面积。如下图所示：
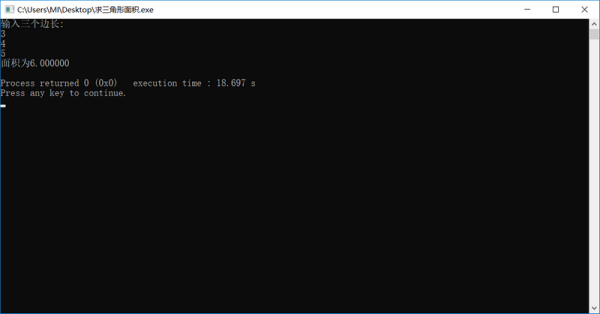
四、在编程判断a,b，c的值能否构成一个三角形，若能构成三角形，则计算并输出三角形的面积，否则输出“不能构成三角形”。已知构成三角形的条件是：任意两边之和大于第三边。如下图所示：
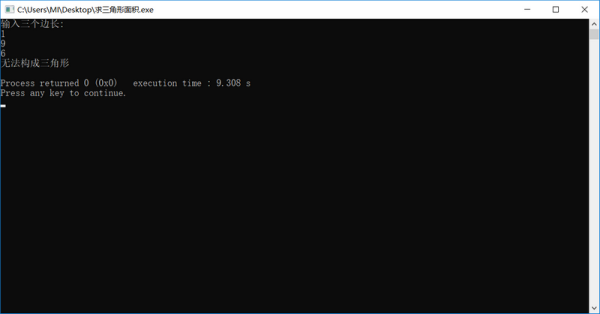
扩展资料
一、此题是海伦公式在C语言中的应用，海伦公式是：
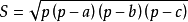
公式中a，b，c分别为三角形三边长，p为半周长，S为三角形的面积。
二、相传这个公式最早是由古希腊数学家阿基米德得出的，而因为这个公式最早出现在海伦的著作《测地术》中，所以被称为海伦公式。
中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”，虽然它与海伦公式形式上有所不同，但它完全与海伦公式等价，它填补了中国数学史中的一个空白，从中可以看出中国古代已经具有很高的数学水平。
三、海伦公式的提出为三角形和多边形的面积计算提供了新的方法和思路，在知道三角形三边的长而不知道高的情况下使用海伦公式可以更快更简便的求出面积，比如说在测量土地的面积的时候，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案。
参考资料来源：
百度百科-海伦公式
小面包
2024-04-25 03:19:16
1、公式：area = sqrt(s*(s-a)*(s-b)*(s-c))
2、代码：
printf("依次输入a,b,c(空格识别一个数)：");
scanf("%f%f%f,",&a,&b,&c);
s=(float)0.5*(a+b+c);
area = (float)sqrt(s*(s-a)*(s-b)*(s-c));
printf("面积为：%f",area);
}
扩展资料
举例： a=3.67;b=5.43; c=6.21;
1、int main()
{
double a, b,c,s,area;//定义三角形的边长和面积
a=3.67;b=5.43;c=6.21;s=(a+b+c)/2;
2、area=sqrt(s*(s-a)*(s-b)*(s-c));//求三角形面积，sqrt表示求根号函数，
printf("a=%f\tb=%f\tc=%f\n",a,b,c);//输出边长
printf("area=%f\n",area);//输出面积
return 0;
}
参考资料
百度百科-C语言
你是我所有的梦
2024-04-25 00:47:03
#include<math.h>
void main()
{
float a,b,c,s,area;
printf("依次输入a,b,c(空格识别一个数)：");
scanf("%f%f%f,",&a,&b,&c);
s=(float)0.5*(a+b+c);
area = (float)sqrt(s*(s-a)*(s-b)*(s-c));
printf("面积为：%f",area);
}
代码如上 很简单的 自己多动手
傲骨
2024-04-25 04:56:01
int main()
{
float a,b,c;
float s,area;
printf("请分别输入a,b,c:");
scanf("%f%f%f",&a,&b,&c);
s=(a+b+c)/2;
if(a>0&&b>0&&c>0){
area=sqrt(s*(s-a)*(s-b)*(s-c));
if(a+b>c&&a+c>b&&b+c>a){
printf("%.2f",area);
}else{
printf("您输入的数据无法构成三角形！");
}
}else{
printf("您输入的数据无法构成三角形！");
}
printf("\n");
return 0;
}
热门标签
